
In order to be accessible to the program during processing, data must be stored in core storage. Thus, input job data is read by an input device, stored in core storage, and then processed. Results (output data) are sent to an output device.
Input data can be represented in a variety of ways depending upon the input medium used. A medium is the material on which data is recorded. For example, a card that is punched with holes (which represent data) is a medium; the card can be read by a card reader. (Refer to subsequent sections for descriptions of the various input devices and the media they use.)
In the 1130 system, data is read from or stored in core storage on a word basis. A word is made up of sixteen positions, numbered 0 to 15.
Position ---> 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
The left-most position (0) is called the high-order position; the right-most position (15) is called the low-order position.
Each position can be at a value of 0 (also called off) or 1 (also called on). For example, all 16 positions of a word can be:
Position ---> 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Value ------> 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
Or:
Position ---> 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Value ------> 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
Or, any combination is possible:
Position ---> 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Value ------> 1 0 0 0 1 1 0 1 0 1 1 1 0 0 0 1 |
Or 0 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 |
Or 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 |
Each position within a word in core storage is called a bit. Numeric, alphabetic, special-character, or logical information can be represented by the bit values in a word. Both the combination of the bits in a word and the intention of the programmer who organizes the program and data in core storage determine whether the data is numeric, alphabetic, special-character, or logical.
Numeric computations in the 1130 system are performed in binary arithmetic by the arithmetic instructions. In other words, the 1130 operates on binary data to produce binary results.
Position 0 (the high-order position) of a word specifies whether the rest of the word contains a positive or negative number. If position 0 is at a value of 0, then the number in the rest of the word is positive; if position 0 is at a value of 1, then the number in the rest of the word is negative.

The assumption has been made that the reader can when given a numeric value represented by the symbols in the binary, hexadecimal, or decimal numbering system convert those symbols to an equivalent numeric value in any of the same systems. For example, the reader should be able to convert the binary symbols 11100010 to the hexadecimal symbols E2 or to the decimal symbols 226. The reader should also be able to do simple addition or subtraction with numeric values represented by binary or hexadecimal symbols. Refer to Number Systems, Order No. SC20-1618, for basic information on binary and hexadecimal numbering systems.
Numeric data can be handled in either single or double precision. Single precision is the single word binary format just described, where bit 0 is the sign bit and bits 1 through 15 contain a numeric value.
When a binary number is contained in two successive words in core storage, with the sign in the leftmost position of the leftmost word, then that number is in double precision format. The left most word of the pair of words must be at a core-storage location that has an even address.
Single Precision Format |
Double Precision Format |
Programming Note: A double-precision number may be stored in core storage starting at an odd address. But instructions that process double-precision operands use two successive words only if an even address is specified. If an odd address is specified, the operation is performed with the odd word twice. Anyone programming the machine to operate in this unusual manner should have an intimate understanding of the internal workings of the 1131 CPU.
Notice that only one sign position is used out of the 32 available positions in the double-precision format. In single precision, one position is used for the sign and 15 positions for the number. The ranges of numeric values that can be represented in single and double precision formats are shown in binary and decimal system symbology in Figure 4.
In Figure 4, negative numbers are in two's-complement binary form; the sign position, at a value of one, signifies the negative number. For example, the single precision number 1111 1111 1111 1111 is shown in Figure 4 as having an equivalent decimal value of -00001 (the left zeros are shown merely to maintain consistency between the binary and decimal notation shown). But this binary value is really the two's complement of negative 1. The true form can be obtained as follows:
Invert (change each position from 1 to 0):
1111 1111 1111 1111
invert
0000 0000 0000 0000
Add 1 to the inverted number:
0000 0000 0000 0000
+1
-------------------
0000 0000 0000 0001
Negative results are always produced in two's-complement form.
|
||||||||||||||
|
||||||||||||||
Figure 4. Numeric Value Ranges for Single and Double Precision Operands
Even though the arithmetic instructions handle data only in the binary formats just listed, other types of arithmetic operations can effectively be performed by use of arithmetic subroutines. These subroutines are part of IBM programming systems and are described in IBM 1130 Subroutine Library, Order No. GC26-5929.
There is no fixed internal character code in the 1131 CPU. Conversions from one bit pattern to another must be performed, however, because many input/output devices are code sensitive. Such conversions must be done by program routines.
In order to print the letter A, for example, a 1403 printer must receive a bit pattern of 1100100 in the output print record. Other bit patterns cause other characters to be printed. The bit pattern to the printer comes from positions 1 through 7 or positions 9 through 15 of a word in core storage (part of an output print record):

If the preceding word is part of a print record to the 1403, then AA is printed at two adjacent print positions.
On the other hand, consider that the bit pattern for the letter A is received in an input record from the 1442 card reader. One core-storage word is required for each card column read by the 1442. The bit pattern for the A from the 1442 is stored into core storage as follows:
Clearly, the bit pattern for the A from the 1442 must undergo some conversion before it can be sent to the 1403 in an output print record.
But even if input data is from the 1442 card reader and output data goes to the 1442 card punch, conversion of bit patterns may be necessary. Assume, as an example, that two fields in an input card record are to be added together, and the result is to be punched into a card as output data. The input data read from the card is in card code, not in binary. This input data must be converted to binary format before the arithmetic instructions can handle it. (Arithmetic instructions operate only on binary data.) Then, after the computation of adding the two numbers, the result must be converted back to card code and sent in an output record to the 1442 card punch.
Note: Any peculiarities or restrictions related to the handling of bit patterns for the 1442, 1403, or other I/O devices are in sections in this book that are devoted to those devices. All conversions of data from one format to another must be program-controlled. Data conversion subroutines are in IBM programming systems for the 1130 system. For descriptions of the data conversion subroutines, refer to IBM 1130 Subroutine Library, Order No. GC26-5929. Programming methods of converting from one data code to another are not described in this functional-characteristics manual.
The various codes used in the 1130 system, via program conversion, are listed in chart form in Appendix A. The Extended Binary Coded Decimal Interchange Code (EBCDIC) shown in Appendix A is an eight-bit code that is given for reference because it is used in other IBM systems (for example, the IBM System/360).
Core-storage capacity is dependent upon the 1131 CPU model but, at a maximum, is 32,768 words (see Figure 3). The address for any core-storage location in an 1131 CPU can be contained in a 16-bit word:
| ADDRESS | ||
| In Binary (16 Bits) | In Hexadecimal | In Decimal |
|---|---|---|
| 0000 0000 0000 0000 | 0000 | 00000 |
| 0000 1111 1111 1111 | OFFF | 4,095 |
| 0001 1111 1111 1111 | 1FFF | 8,191 |
| 0011 1111 1111 1111 | 3FFF | 16,383 |
| 0111 1111 1111 1111 | 7FFF | 32,767 |
The core-storage location specified by address 0000 (hexadecimal) is sequentially next to the highest location in all 1131 models. This means that if a word address that is one greater than the maximum for a particular system is specified, the location accessed is the location specified by address 0000 (hexadecimal). This addressing peculiarity is called wraparound.
In fact, any 16-bit address accesses a core-storage location regardless of the core-storage capacity of the system. The reason for this is that high-order (leftmost) address bits that specify addresses above the capacity of the system are not used and are ignored. For example, in a system that has 4,096 word locations in core storage, the maximum address is:
0000 1111 1111 1111 (for location 4,095 in decimal notation)
The four leftmost bits (for a 4,096 word capacity system) are ignored during actual addressing. Therefore, in this same capacity system, location 4,095 is addressed by all of the following addresses:
0000 1111 1111 1111
0001 1111 1111 1111
0100 1111 1111 1111
and so on.
If you use absolute addresses in conjunction with wraparound, you should be aware of the fact that the core-storage capacity of the system determines the actual location accessed. For example, assume that wraparound from location 4,095 to location 0000 is desired on a minimum capacity system. Wraparound does not occur if the same addresses are used on any other system. On the 4,096-word capacity system, wraparound occurs as follows:
| Binary Address |
Equivalent Decimal Address |
Location Accessed |
|---|---|---|
| 0000 1111 1111 1111 | 4,095 | 4,095 |
| add 1 for wraparound | ||
| 0001 0000 0000 0000 | 4,096 | 0000 |
For an 8,192-word or any larger capacity system, the same addresses result in accessing storage as follows:
| Binary Address |
Equivalent Decimal Address |
Location Accessed |
|---|---|---|
| 0000 1111 1111 1111 | 4,095 | 4,095 |
| add 1 for wraparound | ||
| 0001 0000 0000 0000 | 4,096 | 4096 |
All 1131 CPU's have certain reserved locations in core storage. The reserved locations have the same addresses regardless of the CPU model:
| Core Storage Address | ||
| Hexadecimal | Decimal | Name of Reserved Locations |
|---|---|---|
| 0001 | 00001 | Index-Register 1 (XR1) |
| 0002 | 00002 | Index-Register 2 (XR2) |
| 0003 | 00003 | Index-Register 3 (XR3) |
| 0008-000D | 00008-00013 | Interrupt Vectors |
| 0020-0027 | 00032-00039 | 1132 Printer Scan Field |
You should not use these locations for purposes other than the ones for which they are intended; if you do, you may lose or destroy data. (Subsequent sections of this manual describe the items named in the preceding list.)
There are only two instruction formats in the 1130. The short-instruction format requires 16 bit positions; an instruction in the short-instruction format, therefore, requires one core-storage word location:
Short Instruction

The long-instruction format requires 32 bit positions; an instruction in the long-instruction format, therefore, requires two core-storage word locations:
Long Instruction


Figure 5. Short-Instruction Format
A brief summary of what each group of bits represents in the short-instruction format is shown in Figure 5. Similarly, the significance of bit positions in the long-instruction format is shown in Figure 6. However, you should refer to the description of a specific instruction in order to find out how the bits are used in that instruction. Bits 8 and 9 in the short format, for example, specify the type of shift and not a displacement in certain instructions.
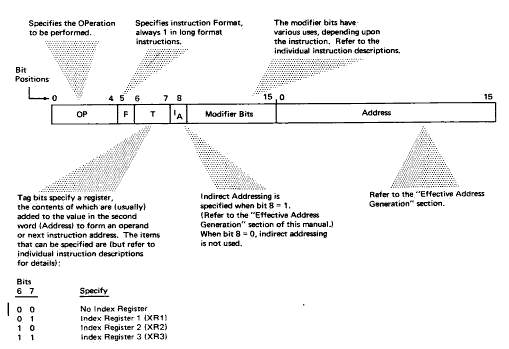
Figure 6. Long-Instruction Format
The actual core-storage location at which specific data (or an instruction) is located is identified by an effective address. In other words, the address of each core-storage location in the 1130 system is called the effective address of that location. For example, the effective address of the data 0404 in the following list is 0001.
| Data (Hexadecimal) |
Core-Storage Word Address (Hexadecimal) |
|
|---|---|---|
| FE01 | 0000 | |
| 0404 | 0001 | |
| 8424 | 0002 | |
| FFFF | 0003 |
The term effective address is used because an address may be directly available or it may be computed, depending upon the operation in progress. The methods of generating effective addresses are different for short and for long format instructions.
In the short-instruction format, the tag (T) bits specify a register as follows:

The value of the displacement (bits 8 through 15 of the instruction) are added to the contents of the specified register. The result of this addition is the effective address:
Specified Register Contents + Displacement = Effective Address
Tag Bits = 00 (Instruction Address Register)
The basic purpose of the instruction-address register is to point to each instruction that is to be executed next. Effective size of the instruction-address register, which is dependent upon the core- storage capacity of the system, is 12, 13, 14, or 15 bits long.
The maximum addresses in the instruction-address register for the various core.storage capacities are:

When the tag bits specify the instruction-address register, the displacement (from the instruction) is added to the current value in the instruction-address register in order to generate the effective address. The instruction-address register at this time contains the address of the core-storage location that immediately follows the instruction being executed.
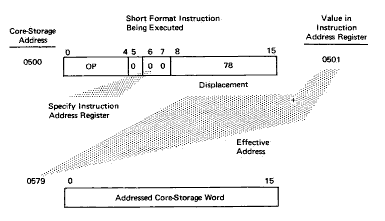
For example, a short instruction from the core-storage location specified by address 0500 is being executed (Figure 7). During execution of this instruction, the instruction-address register is updated automatically to 0501, the address of the core-storage word immediately following the short instruction. The value in the instruction-address register is then 0501 when the effective address is generated.
Further assume that the displacement in the short instruction at location 0500 is:
| Displacement | ||||||||||||||||||
| Binary | Hexadecimal Equivalent | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bit Positions |
|
78 | ||||||||||||||||
 |
||||||||||
|
Figure 7. Positive Displacement (Short-Instruction Address Generation)
Also assume that the core-storage capacity is 4,096 words, and, therefore, the instruction-address register contains 12 bit positions. To form the effective address, the displacement is added to the value in the instruction-address register:
| Binary | |
|---|---|
| 0501 (Hex) from instruction-address register | 0101 0000 0001 |
| 78 (Hex) from displacement in instruction + | 0000 0000 0111 1000 |
| Effective address 0579 (Hex) | 0000 0101 0111 1001 |
The effective address is displaced by a value of 78 from the current value (0501) of the instruction- address register. This is why bits 8 through 15 of the instruction are called the displacement.
In the preceding example, the value of the high-order (leftmost) bit of the displacement is propagated to the left to form a 16-bit operand (0000 0000 0111 1000) and then added to the value from the instruction-address register. This is a normal operation that determines whether the displacement is positive or negative with respect to the value in the instruction-address register.
The eight available bits in the short instruction, which collectively form the displacement, provide a range from -128 words (decimal) to +127 words (decimal) of addressing capability. Whether the displacement is positive or negative is determined by the value of bit eight — the leftmost bit of the displacement in the instruction. When bit 8 = 0, the displacement is positive:
| Positive Displacement Value | ||
| Binary | Decimal Equivalent | |
| Current value in instruction-address register + | 0000 0000 | 000 |
| to | to | |
| 0111 1111 | 127 | |
When bit 8 = 1, the displacement is negative:
| Positive Displacement Value | ||
| Binary | Decimal Equivalent | |
| Current value in instruction-address register + | 1111 1111 | -1 |
| to | to | |
| 1000 0000 | -128 | |
The value in the instruction-address register is always considered positive, even if its leftmost bit is at a value of 1.
Tag Bits = 01, 10, or 11 (Index Register 1, 2, or 3)
When an index register is specified, address generation is similar to that used when the instruction-address register is specified. Two basic differences, however, are:
Any index register can be loaded by the program with either a negative (bit 0 = 1) or a positive (bit 0 = 0) value. For the addressing scheme described here, however, the value in the index register is always considered positive; high-order, unused bits beyond the capacity of the system are ignored (refer to Core Storage Addresses").
Figure 8 is an example of a negative displacement used with the contents of an index register to form an effective address.
Two types of addressing are defined for long-format instructions: direct and indirect addressing. An effective address generated in the manner already described for short-format instructions is called a direct address -- short-format instructions, in fact, can perform only direct addressing.
The indirect address (IA) bit (bit 8) in long-format instructions specifies whether addressing is direct or indirect:
| Indirect Address (IA bit 8) |
Type of Addressing |
|---|---|
| 0 | direct |
| 1 | indirect |
Direct Addressing (IA Bit 0)
Here the tag bits can specify an index register (1, 2, or 3) as in short-format addressing, or no index register (0). The instruction register is not used to compute the effective-address as it is in the short-format instructions.
When an index register is specified, the second word (address field) of the long-format instruction is added (Figure 9) to the value in the index register to form the effective address.
Indirect Addressing (IA Bit = 1)
In indirect addressing, some word location in core storage contains a value that is the effective address. The desired effective address must be program-loaded into the word. This location, which can be any word in core storage, is itself first addressed by direct addressing. Then the contents of that word become the effective address (Figure 10).
When the tag bits equal 00, as in direct addressing in long-format instructions, the core-storage word that contains the effective address is located by the value in the address field in the instruction.

Figure 8. Negative Displacement
 |
||||||||||
|
Figure 9. Direct Addressing (Long-Format Instruction)
Exceptions to the general schemes of addressing are shown in Figure 11.
Short-Format Instructions (F=0)
| Tag Bits | Specified Register | Effective Address (EA) |
| T=00 | Instruction-Address Register (IAR) | EA = IAR + Displacement |
| T=O1 | Index-Register I (XR1) | EA = XR1 + Displacement |
| T=1O | Index-Register 2 (XR2) | EA = XR2 + Displacement |
| T=11 | Index-Register 3 (XR3) | EA = XR3 + Displacement |
The high-order (leftmost) bit of the displacement determines whether the displacement is effectively added to or subtracted from the contents of the specified register:
| Short Format Bit 8 Value (Leftmost Bit of Displacement) |
Effective Operation |
| =0 | Add displacement |
| =1 | Subtract displacement (complement add) |
The displacement range is -128 to +127 (decimal) word locations from the value in the specified register.
Long-Format Instructions (F=1)
| Direct Addressing (IA=0): | ||
| Tag Bits | Specified Register | Effective Address (EA) |
| T=00 | None | EA = Address field |
| T=01 | Index-Register I (XR1) | EA = XR1 + Address field |
| T=10 | Index-Register 2 (XR2) | EA = XR2 + Address field |
| T=11 | Index-Register 3 (XR3) | EA = XR3 + Address field |
High-order (leftmost) bits in the generated effective address that are beyond the storage capacity of the system are ignored.
Indirect Addressing (IA 1): A core-storage word location is specified. The contents of that word are the effective address. The core-storage word is specified in the same manner as that just described in direct addressing.

Figure 10. Indirect Addressing (Long-Format Instructions Only)
| Instruction | Short Format | Long Format | |
|---|---|---|---|
| IA=0 | IA=1 | ||
| LDS | The values of bits 14 and 15 of the instruction are used to set/reset the carry and overflow indicators. | -------------------- |
-------------------- |
| LDX | The expanded displacement (16 bits) is loaded into IAR, XR1, XR2, or XR3. | The address field is loaded into IAR, XR1, XR2, or XR3. | The contents of the storage location specified by the address field are loaded into AR, XR1, XR2. or XR3. |
| MDX | The expanded displacement (16 bits) is added to IAR, XR1. XR2. or XR3. | Tag=00: The expanded displacement (16 bits) is added to the contents of the storage location specified by the address field. Tag != OO: The contents of the address field are added to the index register specified. |
Tag=OO: The expanded displacement (a 16-bit negative number) is added to the contents of the storage location specified by the address field. Tag != O0: The contents of the storage location specified by the address field are added to the index register specified. |
| Shift Instructions | The number of shifted positions is controlled by the contents of the six low-order bits of the displacement (or register, if specified). | -------------------- |
-------------------- |
| STX | The effective address is obtained by adding the displacement to the IAR. | The address field is the effective address. | The contents of the storage location specified by the address field is the effective address. |
| WAIT | The displacement is not used. | -------------------- |
-------------------- |
| IAR = Instruction Address Register | |||
| XR1 Index Register 1 | |||
| XR2 = Index Register 2 | |||
| XR3 = Index Register 3 | |||
Figure 11. Exceptions to Effective Address Generation
Instruction-Address Register
The instruction-address register holds the address of the next instruction to be executed. For example, assume that the following instruction is being executed:
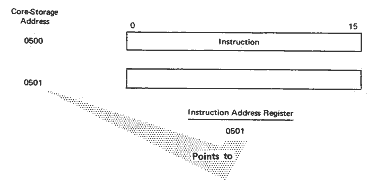
The instruction-address register contains the address of the core-storage word immediately following the instruction being executed. In most cases, this next word is the next instruction to be executed. Sometimes, however, the contents of the instruction-address register are changed as a result of the instruction being executed. Execution of a branch instruction, for example, can cause accessing of the next instruction from a core-storage location other than the one immediately following the current instruction.
The effective size of the instruction-address register depends upon the core-storage capacity of the system:
| Effective Size of Instruction- Address Register (Bits) |
Core-Storage Capacity (Words) |
| 12 | 4,096 (decimal) |
|---|---|
| 13 | 8,192 |
| 14 | 16,384 |
| 15 | 32,768 |
In short-format instructions when the tag bits equal 00, the contents of the instruction-address register are used in effective address generation.
Index-Registers 1, 2 and 3
Index-registers 1, 2, and 3, each of which is a 16-bit word location in main storage, are used in address generation during instruction execution. Refer to Effective Address Generation for a description of addressing concepts.
Each index register, just as any other core-storage word, can contain a positive or negative number. When bit 0 = 0, the number is positive; when bit 0 = 1, the number is negative.
Accumulator (ACC)
This 16-bit register is used in arithmetic, shift, logical, and I/O operations.
In arithmetic operations, the accumulator is program-loaded with one of the two operands. Next, the operation is performed using one operand from core storage and the other from the value loaded into the accumulator. The result is in the accumulator at the end of the operation. Loading an operand into the accumulator and then specifying, in an arithmetic instruction, the operation and the location of the other operand in core storage are program-controlled operations. Development of the result in the accumulator is a machine function that is dependent upon the arithmetic instruction that is executed. The process is summarized in Figure 12. For arithmetic operations with 32-bit operands or 32-bit results, the accumulator and an accumulator extension are used (see Accumulator Extension).
The accumulator can be loaded from any core-storage word by a load-accumulator instruction. Contents of the accumulator can be stored into any core-storage word by a store-accumulator instruction.
Refer to the specific instruction descriptions for discussions of the ways in which the contents of the accumulator can be manipulated in shift and logical operations.
The accumulator is also used during I/O operations to hold status information. The status information indicates such conditions as:
Status words are of two types: the interruption level status word (ILSW) and the device status word (DSW). A status word, ILSW or DSW, is loaded into the accumulator under program control. (The ILSW's and DSW's are described elsewhere in this manual.)
Accumulator Extension (0)
This 16-bit register is used in arithmetic operations when 32-bit operands are used or 32-bit results are produced. The extension is to the right of the accumulator:

For descriptions of how the accumulator and accumulator extension function together, refer to the sections of this manual devoted to the following instructions:
| Instruction | Mnemonic |
|---|---|
| Add double | AD |
| Divide | D |
| Load double | LDD |
| Multiply | M |
| Rotate right ACC and EXT | RTE |
| Shift left ACC and EXT | SLT |
| Shift left and count ACC and EXT | SLC |
| Shift right ACC and EXT | SRT |
| Store double | STD |
| Subtract double | SD |

Figure 12. Use of the Accumulator in Arithmetic Operations
Carry and Overflow Indicators
Operations that affect the carry and overflow indicators are summarized in Figure 13.
The overflow indicator specifies when results of arithmetic operations exceed the capacity of the accumulator or accumulator plus accumulator extension.
The carry indicator is most useful in shift and logical operations. It can also be useful in program routines where arithmetic results may exceed the capacity of the accumulator and its extension (in double-precision arithmetic).
| Instruction | Carry Indicator | Overflow Indicator |
|---|---|---|
| A | Set to zero prior to execution; set to one by a carry out of the high-order bit position of the accumulator. | Set to one if sum is greater than the capacity of the accumulator, If the overflow indicator is on before execution, its condition is not changed regardless of the result. |
| AD | Same as A. | Same as A. |
| BSC or BOSC | Not affected when tested. | Reset when tested. |
| BSI | Not affected in short format; not reset if tested in long format. | Not affected in short format; reset when tested in long format. |
| D | Not set, not reset. | Set to one when an attempt is made to divide by zero, or set to one when a quotient overflow occurs. |
| LDS | Set to the value of bit 14 of the instruction. | Set to the value of bit 15 of the instruction. |
| S |
Set to one when a borrow occurs beyond the high-order position of the accumulator. Set to zero prior to execution of the instruction. |
Same as A. |
| SD | Same as S. | Same as A. |
| SLA | Set to one if the last bit shifted out of the high-order position of the accumulator is a 1; set to zero if the same bit is a 0. | Not set, not reset. |
| SLC | Same as SLCA. | Not set, not reset. |
| SLCA | Set to one if the shift is terminated by a 1-bit in the high-order position of the accumulator; set to zero if the shift is terminated by the count (in CCC) going to zero (even if a 1-bit is in the high-order position of the accumulator). | Not set, not reset. |
| SLT | Same as SLA. | Not set, not reset. |
| STS | Set to zero. | Set to zero. |
| Note: Instructions not listed in this figure do not affect the carry and overflow indicators. | ||
Figure 13. Effect of Instruction Execution on Carry and Overflow Indicators
The actual value of an arithmetic result that exceeds the capacity of the accumulator and its extension can be determined through combined testing of the carry and overflc~ indicators. In the following illustrative examples, only four bit positions are used to demonstrate the principle (the accumulator and its extension in reality hold 32 bits):
| Example 1 | ||
| Operation Add |
Operand 7 (hex) |
Operand 7 (hex) |
|---|---|---|
| In binary notation: | In hexadecimal notation: | |
| 0111 | 7 | |
| +0111 | +7 | |
| 1110 | E | |
In example 1, no carry occurs out of the high-order position. An overflow occurs because the result is negative (indicated by a value of 1 in the sign bit -- the leftmost bit). The desired result of the addition, however, is a positive number. This can be achieved by appending (via programming) a high-order zero to the answer: 01110. In this example, the overflow indicator is on as a result of the operation, but the carry indicator is off.
| Example 2 | ||
| Operation Add |
Operand -8 (hex) |
Operand -8 (hex) |
|---|---|---|
| In binary notation: | In hexadecimal notation: | |
| 1000 | -8 | |
| +1000 | +-8 | |
| C 0000 | -10 | |
In example 2, both a carry-out (C) and an overflow occur. Therefore, both the overflow and carry indicators are on as a result of the operation. Because the carry indicator is on, a high-order 1 should be appended to get the desired result (in two's-complement form): 10000.
| Example 3 | ||
| Operation Subtract |
Operand -8 (hex) |
Operand +7 (hex) |
|---|---|---|
| In binary notation: | In hexadecimal notation: | |
| 1000 | -8 | |
| -0111 | -+7 | |
| B 0001 | -F | |
In example 3, a borrow (B) beyond the high-order position and an overflow occur. Therefore, a high-order 1 should be appended to the result. (The result is in two's-complement form.)
The registers described here are not under direct program control but function automatically as required by the operation in progress. Contents of these registers can be displayed in indicators on the system console. Figure 14 shows the position of the registers in the CPU data flow.
Arithmetic-Factor Register (AFR)
This 16-bit register holds one operand during arithmetic and logical operations. (The other operand is in the accumulator.) The arithmetic-factor register is also referred to as the D register.
Cycle-Control Counter (CCC)
The cycle-control counter is a 6-bit register that is used primarily to count CPU cycles and control shift operations.
Operation Register (OP)
This 5-bit register holds the operation code of the instruction being executed.
Storage-Address Register (SAR)
The storage-address register contains the address of each location that is accessed in main storage, except for data transfers for cycle-steal I/O devices. Such devices provide main-storage addresses in circuitry separate from the storage-address register. The storage-address register is 12, 13, 14, or 15 bit positions in size, depending upon the core-storage capacity of the system. The SAR is also referred to as the M register.
Storage-Buffer Register (SBR)
This 16-bit register is the buffer between the CPU and core storage. Every word of data transferred to or from core storage passes through the storage-buffer register. The storage-buffer register is also called the B register.
Operation-Tag Register (TAG)
With a 3-bit capacity, the TAG register contains the F (format) and T (tag) bits of the instruction being executed. The format bit determines the instruction length (short or long) and the tag bits select the index register.
Temporary Accumulator (TAR)
This 16-bit register, which is the image of the accumulator, is used to store the contents of the accumulator during effective-address computation. The temporary accumulator is also referred to as the U register.

Figure 14. CPU Controls and Data Flow
But wait, there's MORE...